Система встреч с удивительными предметами, разгадывание способов их создания – все это позволяет обеспечить интерес и продуктивность в поисковой деятельности младших школьников. Для компенсации информационных перегрузок и с целью пробуждения поисковой активности наилучшим способом включения учеников в работу являлся акт удивления или как его называют «эффект чуда». Этот блок состоит из двух заданий.
Задание – Вставьте пропущенное слово.
№1. АРГОН (РОЗА) ГРОЗА
АТЛЕТ (_________) НОРМА
№2. ПЛАН (РАНГ) ТОРГ
СЕНО (________) СПАД
№3. КОРА (КОЗА) АЗОТ
КЛЕН (_______) ПИЛА
Задание – Решить анаграмму и исключить лишнее.
САИВЛ
РЕОХ
ШПАУГ
ШРАУГ
Учитель обращается к детям:
Здравствуйте, ребята. Один мой знакомый пятиклассник сказал, что дроби он не понимает, изучать не хочет, потому что в жизни они ему не пригодятся. А вы как думаете? Где вы сталкиваетесь в жизни с дробями? А дома у вас имеются дроби?
Сегодня на уроке мы с вами еще раз убедимся, что дроби и математика нас окружает повсюду.
Далее учитель сообщает тему, ставит задачи урока и объясняет, что работа будет традиционно проходить в группах, задача каждой команды набрать наибольшее количество баллов.
Затем учитель берет в руки шкатулку и говорит: «Здесь что-то, что имеет отношение к вам, математике и нашему уроку. Как вы думаете, что это? Если вы будете хорошо работать, я буду вам делать подсказки, и вы догадаетесь».
Прежде, чем мы начнем работать, традиционно предлагаю творческое задание. (Выбрать, кому достанется творческое задание, это тоже творческий процесс: можно считалочкой, можно спросить у одного из учеников любимое число от 1 до 24 и выбрать ученика под таким номером в списке журнала и т. д.) Итак, Иванов получил творческое задание и готовит его 3 минуты в отведенном месте: за отдельной партой, за дверью в коридоре и т. д. (На данном уроке творческое задание было записано на карточке в конверте: «Дорогой друг, через 3 минуты тебе нужно перевоплотиться в профессора математики, зайти в класс и провести опрос, задав 5 самых важных вопросов по теме «Дроби»).
Учитель в это время задает задачи.
1. Найдите дробь, у которой числитель меньше знаменателя и которая не изменяется, если ее запись перевернуть «вверх ногами».
2. Как от куска материи в 2/3 метра отрезать полметра, если под руками ничего нет?
Зная определения тригонометрических функций угла в прямоугольном треугольнике, попробуем расширить эти понятия не только для острого угла, но и для любого угла, выраженного в радианах.
Известно понятие координатной прямой. Координатная прямая задана, если на произвольной прямой выбрано начало измерения и положительное направление откладывания чисел. 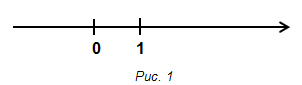
Вопрос – существуют ли другие координатные линии, на которых можно было бы откладывать заданные числа?
Предложения учащихся: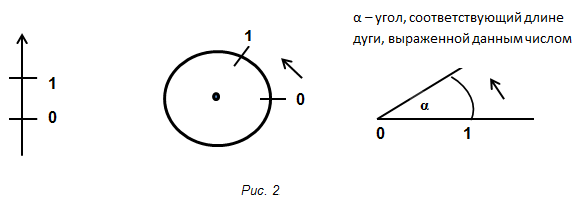
Учащиеся знают понятие координатной прямой: прямая, имеющая начало отсчета, единицу измерения и положительное направление отсчета чисел. Им предлагается придумать свою координатную линию, на которой можно было бы откладывать точки, соответствующие заданным числам, причем числа эти должны иметь вид:
![]()
После обсуждения предложений учащихся и выбора единичной окружности как координатной линии и выбора единичного отрезка логичного переходим к следующему блоку.
На данном этапе учащимся предлагается рассмотреть удивительные объекты и дать характеристику каждого из них (рис. 1).
На данном занятии используется игра «Сундучок знаний». Карточки из набора «Великие изобретения» содержат в себе интересные сведения и факты об основных научных изобретениях и открытиях, сделанных за всю историю человечества. Из карточек дети узнают когда, кем и в какой стране было сделано изобретение, наиболее любопытные факты о нём и то, насколько важным оно стало для человечества. Игра тренирует память, развивает наблюдательность и внимательность.