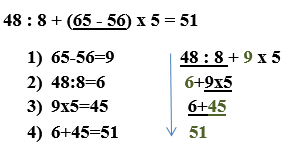Данный эффект может быть использован на уроке истории в 5-м классе по теме "Театр в Древней Греции"
Начало урока: на доске закрытые две фотографии (это интрига урока). Учитель говорит детям, что на этих фотографиях люди, которых они знают…
Но вот какое отношение они имеют к теме урока? Об этом мы узнаем позже.
Продолжается урок, детям рассказывают о том, как выглядел театр, кто в нем играл, какие пьесы.
Время от времени учитель напоминает детям о фотографиях и спрашивает, не догадываются ли они, кто изображен. Очень много предположений, но верных пока нет.
В конце урока интрига раскрывается, учитель открывает фотографии, на них Чехов и Верка-Сердючка. Итак, какое же отношение эти люди имеют к театру?
Правильно. Чехов написал всемирно известные пьесы, а его брат Михаил создал театральную школу. Верка-Сердючка – это мужчина, играющий женскую роль на сцене, как это делали в древнем греческом театре.
В начале урока показываю детям вырезку из газеты, в которой нам предлагают выиграть миллион.

Этот эффект удивления показываем на уроке физкультуры и применяем в нашей жизни.
Прежде чем проводить этот опыт с детьми, задайте вопрос: «Как можно проткнуть варенную картофелину соломинкой, чтобы соломинка не сломалась?»
Выслушав все ответы, возьмите соломинку большим и указательным пальцами, проткните картофелину под нужным углом. Нужно потренироваться заранее, чтобы научиться это выполнять. Потому что нужен определенный угол наклона и определенное усилие, чтобы все получилось. Предоставьте возможность всем попробовать проделать эксперимент, и дети сами убедятся, что проткнуть картофелину получится лишь тогда, когда будет нужный угол наклона соломинки и приложено нужное усилие.
То же самое происходит, когда мы сталкиваемся с трудной ситуацией, которая кажется нам безвыходной. Поэтому безвыходных ситуаций не бывает!
Этот эффект удивления показываем на уроке физкультуры и применяем в нашей жизни.
Прежде чем проводить этот опыт с детьми, попробуйте найти нужное расстояние, на котором вы будете держать свечу и нужное количество воды для шарика.
Наполните один шарик водой так, чтобы она покрыло дно. Надуйте шарики одинакового размера. Зажгите свечу.
Спросите детей, что станет с шариками, если их поместить над пламенем. Затем пустой шарик держите над свечой и посмотрите, как он лопнет. Спросите детей: "Защитило что-нибудь шарик ? Почему нет ?"
Подержите второй шарик над огнем. Следите внимательно, он не лопается.
Погасите свечу. Порассуждайте: "Почему шарик не лопнул?"
Может шарик быть символом тех, кто занимается физкультурой и спортом. У людей, которые ведут здоровый образ жизни есть что-то внутри, что хранит их от болезней и они имеют защиту.
Когда мы занимаемся физкультурой и спортом, то мы защищены от болезней, как шарик от пламени свечи.

– Во второй строчке «спряталось» действие вычитание в скобках, вместо него появилась «9»-разность.
– В третьей строчке «исчезло» действие деление, вместо него появилась «6» -частное.
– Четвёртая строчка «прячет» действие умножение 9 х 5, получается 45.
– Последняя строчка показала сумму 51, а «спрятала» слагаемые 6 и 45.